In a new study, researchers from IBM® and Vanguard explore how quantum computing can tackle one of the most computationally demanding problems in finance: constructing optimized portfolios under real-world constraints. The work, which leverages what’s known as a sampling-based variational quantum algorithm (VQA), shows that quantum-classical hybrid workflows have the potential to provide solutions on par with purely classical methods for complex financial optimization tasks—paving the way for future applications in asset management and beyond.

The challenge of portfolio construction

Portfolio construction is the process of selecting a mix of financial assets—for example, stocks or bonds—that meet specific investment goals. The most well-known approach is the Markowitz model, first introduced by economist Harry Markowitz in the 1950s, which balances expected return against risk (typically measured as “variance”) to identify so-called “efficient” portfolios. These portfolios lie on what we call the efficient frontier, meaning they offer the best possible return for a given level of risk.

However, the Markowitz model makes several simplifying assumptions: it treats returns as normally distributed, assumes perfect knowledge of risk and return estimates, and often ignores real-world constraints like transaction costs, liquidity, or regulatory limits. In practice, portfolio managers must navigate a far more complex landscape. That landscape might involve discrete decisions such as whether to include a specific bond or not, nonlinear constraints such as constraints which may include interactions between assets held in the portfolio (e.g., risk), and multiple competing objectives such as cases where the goal is to both maximize return while also minimizing risks.

As the number of candidate assets grows, often into the thousands, the optimization problem becomes exponentially harder. Classical solvers can struggle to find high-quality solutions within a timeframe that is practical for real-world use cases. This is especially true when the problem includes elements that increase computational complexity, such as general integer variables, clustering constraints, and non-convex objectives.

A new paradigm: quantum optimization

In their work, the IBM-Vanguard team explore how sampling-based variational quantum algorithms may be able to address this challenge. These methods combine the strengths of quantum sampling with classical optimization and post-processing, enabling a new class of heuristics that can explore complex solution landscapes more efficiently than traditional methods.

Heuristics are algorithms that do not offer the same performance guarantees as exact methods. Exact methods are designed to find the absolute optimal solution to a problem, even when doing so requires millions of years and infinite computational resources. To boost efficiency, heuristic algorithms aim for “good-enough” solutions that are often based on a deep intuitive understanding of a considered problem, or which are derived from running exact optimization algorithms and terminating them prematurely.

Heuristics have proven to be so valuable that they now comprise nearly all of the classical optimization algorithms that we use for real-world applications. Researchers have good reason to believe that heuristic methods such as variational quantum algorithms will play a vital role in the emerging paradigm of quantum optimization as well.

Exploring the power of variational quantum algorithms

Variational quantum algorithms are a class of quantum algorithms that combine quantum and classical computational resources in an iterative loop to find solutions to problems. They are specifically designed for today’s quantum devices, which are sensitive to environmental noise and other disturbances that can cause errors in their computations. Unlike algorithms that require fault-tolerant quantum computers capable of correcting errors as they arise during computations—such as Shor’s algorithm for factoring, or quantum phase estimation—VQAs with noise mitigation schemes can be executed on current hardware.

Rather than relying on deep circuits or long coherence times, VQAs use relatively simple, flexible quantum circuits that are trained using classical optimization loops. This makes them particularly well-suited for optimization problems, where the goal is not to compute an exact answer, but to find a solution that is good enough for practical use cases.

In this study, the team used 109 qubits of the 133 available on an IBM Quantum Heron r1 processor, executing circuits with up to 4,200 gates. The quantum samples were then refined using a classical local search algorithm to further improve solution quality.

Key results

The researchers applied this method to a simplified bond Exchange Traded Fund (ETF) portfolio construction problem. The results were benchmarked against the classical optimization solver CPLEX, which is able to solve the problem to optimality at this scale. Promising metrics were shown, including:

• An optimization gap within accepted industry standards after quantum sampling and local search
• Improved convergence at smaller problem scales when using more entangled quantum circuits, such as the BFCD ansatz (note that at larger scales, such as the 109-qubit case illustrated in the plot below, the advantage of BFCD is hindered—likely due to the deeper and thus more noise-laden circuits)
• Robust performance even in the presence of hardware noise, with sample quality improving over iterations
• Importantly, the study found that the quantum-classical workflow consistently outperformed a purely classical local search approach, especially as problem size increased

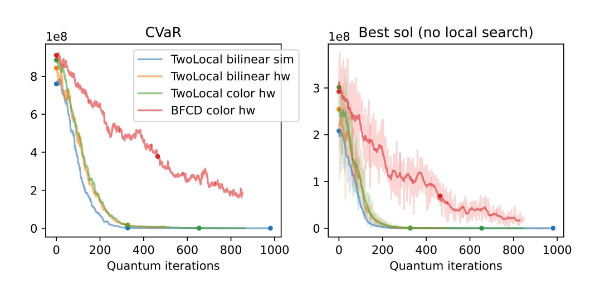
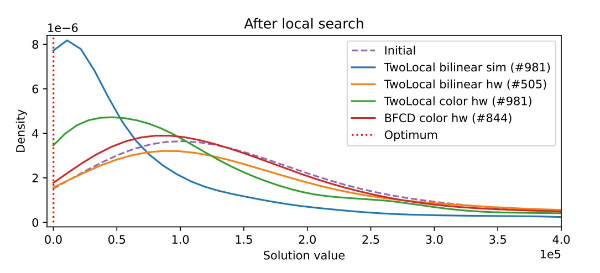
Quantum-classical synergy in action

This work highlights the growing potential of quantum optimization workflows. By combining quantum circuits that explore high-dimensional solution spaces with classical algorithms that refine and validate results, researchers can tackle problems that are too large or too complex for either quantum or classical methods alone.

This approach is particularly promising for domains like finance, where optimization problems are often constrained, nonlinear, and sensitive to small changes in input data. Quantum circuits offer a fundamentally different approach to finding answers to these hard problems—one that may uncover patterns or structures that classical heuristics miss.

Why it matters

This study represents a significant step forward for applications of quantum computing to real-world financial problems. It shows that quantum hardware can already contribute to solving simplified versions of practical optimization tasks. Its existence also shows that financial institutions like Vanguard are actively exploring quantum technologies to enhance decision-making.

As quantum hardware continues to scale and algorithms continue to mature, hybrid workflows hold promise to outperform classical methods for solving complex, constrained problems. It is entirely possible that we will soon see quantum tools integrated into the daily workflows of asset managers, traders, and risk analysts.

Looking ahead, this study opens several exciting directions for future research. For example, researchers could explore better designs for ansatzes, the quantum circuits that generate initial trial states for the VQA's iterative process. This could include new ansatz designs that balance improvements to entanglement (the ability to represent a wide array of complex entangled states) with improvements in trainability (the ability to steer the ansatz towards the optimal solution—which becomes difficult if the ansatz is too complex).