In a collaborative study by Qruise and Quantum Machines, a team of researchers have applied Qruise’s advanced Model Learning algorithms to significantly improve superconducting flux-based entangling gates. By combining data from multiple experiments, the team developed a highly-accurate digital twin of the quantum system in order to reverse engineer signal distortions.

One of the key limiting factors for large scale quantum computing is the fidelity of two-qubit gates, where the fidelity is the accuracy and reliability of the gate executing the desired task to produce the desired outcome. To obtain high gate fidelities, it is very important to accurately know the transfer function (the distortion of the intended signal due to the control electronics). Current approaches to determine the transfer function rely on running a particular experiment called Cryoscope [1]. The input signal to the gates can be reconstructed through careful analysis of the data, and experimentalists design an inverse filter to correct particular aspects of the signal.

The problem with this approach is that it requires specific implementation of the Cryoscope experiment and a specific analysis technique in order to obtain only the transfer function. And while this is not an issue if one wishes to focus only on this particular flux distortion issue, the need to design and implement different experiments for each parameter and physics phenomenon required is onerous. Much of this load can be alleviated with Model Learning.

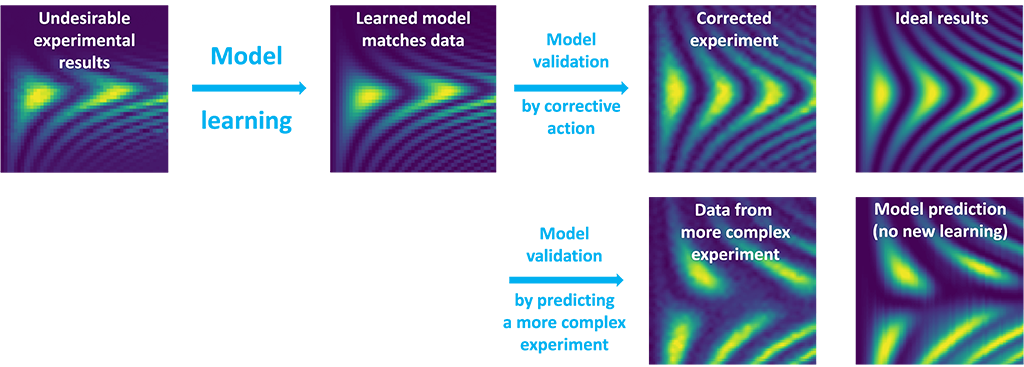
A highly adaptable feature of the Qruise ML, Model Learning can determine any number of system parameters from any relevant experimental dataset by optimizing the model to best fit the data. In this work, the team combined data from multiple experiments to develop a single model describing in detail the control electronics and quantum device and generate a highly accurare digital twin of the system. Focusing on the flux line transfer function, they automatically tuned the model to resolve flux distortion effects, among others, and generate inverse filters to correct for them.

Using this advanced Model Learning algorithm, the team learned 83 parameters from a single chevron plot of a square pulse of varying duration and amplitude. Specifically, the qubit-qubit coupling, flux periodicity, and DC bias were extracted, as well as 80 parameters describing the combination of FIR and IIR transfer functions of the flux line. The learned model was validated three times: first, by performing optimal control on the updated model and inverting the transfer function, thereby enhancing the contrast by 1.5 times; second, by showing the model correctly predicts uncorrected bipolar flux pulses [2]; and third, by correcting the flux-line distortions by correcting the phase shifts and enhancing contrast by 10%.

As high fidelity quantum gates require the interaction between qubits to be very precise, it’s necessary to use a perfectly designed control pulse. Due to the extremely high accuracy of their model, the team were able to design an optimal filter that corrected for the system distortions, significantly improving upon the Cryoscope method.

These results from Qruise and Quantum Machines are highly significant and will likely be of great use in the development of high fidelity two-qubit gates and beyond. Part of the beauty of the technique is how versatile it is, allowing the determination of an arbitrary set of model parameters from any set of relevant experimental data. Although this particular study focused on flux-based two-qubit superconducting gates, the method could easily be generalised to different types of gates and indeed different systems. “Applied widely, Model Learning can help obtain a predictive detailed model of quantum hardware, allowing researchers to not only obtain the best fidelities possible for a given system, but also determine a detailed error budget,” says Shai Machnes, CEO of Qruise. “This error budget provides researchers with actionable information as to which physical factors are limiting gate fidelities, allowing for maximum performance enhancement between successive device iterations.”​​​​